D-FINE: REDEFINE REGRESSION TASK IN DETRS AS FINE-GRAINED DISTRIBUTION REFINEMENT

总结与动机

实时物体检测的需求日益增长，YOLO 系列和 DETR 是当前两种主流的实时检测器。YOLO 系列以其效率和强大的社区生态系统而闻名。DETR 基于 Transformer 架构，具有全局上下文建模和直接集合预测的优势，无需非极大值抑制 (NMS) 和锚框。然而，DETR 通常受到高延迟和计算需求的限制。尽管已经有了RT-DE

现有检测器在边界框回归的公式化、定位不确定性建模以及知识蒸馏效率方面存在挑战。

🎉 D-FINE通过重新定义DETR模型中的边界框回归任务，引入了细粒度分布优化（FDR）和全局最优定位自蒸馏（GO-LSD），实现了卓越的定位精度。 🚀 FDR将回归过程从预测固定坐标转换为迭代优化概率分布，提供了细粒度的中间表示，而GO-LSD则通过自蒸馏将定位知识从深层传递到浅层。 🏆 在COCO数据集上，D-FINE-L/X在NVIDIA T4 GPU上分别以124/78 FPS的速度实现了54.0%/55.8%的AP，并在Objects365上预训练后分别达到57.1%/59.3%的AP，超越了所有现有的实时检测器。

细粒度分布优化 (FDR)

传统方法的局限性：传统的目标检测中的边界框回归通常使用 Dirac delta 分布来建模，无论是基于中心点 {x, y, w, h} 还是基于边距离 {c, d} 的形式。其中，d = {t, b, l, r} 表示从锚点 c = {xc, yc} 到上下左右边的距离。Dirac delta 分布假设边界框的边缘是精确和固定的，这使得模型难以处理定位的不确定性，尤其是在模糊的情况下。这种刚性的表示方式不仅限制了优化过程，还会导致小的预测偏差引起显著的定位误差。

GFocal 的改进：为了解决这些问题，GFocal (Generalized Focal Loss, Generalized Focal Loss v2) 使用离散的概率分布来回归从锚点到四个边缘的距离，从而提供了一种更灵活的边界框建模方式。

具体来说，GFocal 的建模过程如下：

1. 距离表示：对于每个锚点，GFocal 预测从该锚点到边界框四个边缘的距离，即上 (top)、下 (bottom)、左 (left)、右 (right)，表示为 $d = \{t, b, l, r\}$。

2. 离散概率分布：与直接预测一个固定的距离值不同，GFocal 为每个距离预测一个离散的概率分布。这意味着对于每个边缘，模型会预测一组离散值的概率，而不是一个单一的值。

3. 公式表达： GFocal 使用以下公式来计算边界框距离 $d$：

   $$d = d_{max} \sum_{n=0}^{N} \frac{n}{N} P(n)$$

   其中： $d_{max}$ 是一个标量，用于限制从锚点中心到边缘的最大距离。这个值定义了模型能够预测的最大范围。 $N$ 是离散区间的数量，也就是将 $0$ 到 $d_{max}$ 的距离范围划分成 $N$ 个小区间。 $n$ 是离散区间的索引，从 $0$ 到 $N$。 $P(n)$ 表示第 $n$ 个离散区间的概率。这个概率值表示了模型认为真实距离落在该区间的可能性。

4. 概率加权求和：

   • 公式中的 $\sum_{n=0}^{N} \frac{n}{N} P(n)$ 部分计算的是所有离散区间的概率加权和。每个离散区间的索引 $n$ 除以总区间数 $N$ 可以看作是该区间的一个归一化代表值。
   • 通过将每个区间的归一化代表值乘以其对应的概率 $P(n)$，然后将所有这些乘积加起来，就可以得到一个期望距离值。
   • 最后，将这个期望距离值乘以 $d_{max}$，就可以得到最终预测的距离 $d$。

5. GFocal 存在的挑战：

   • 锚点依赖 (Anchor Dependency)：回归过程依赖于锚框的中心，这限制了预测的多样性，并且与无锚框 (anchor-free) 的框架不兼容。
   • 无迭代优化 (No Iterative Refinement)：预测是一次性的，没有迭代的优化过程，这降低了回归的鲁棒性。
   • 粗糙的定位 (Coarse Localization)：固定的距离范围和均匀的 bin 间隔可能导致粗糙的定位，特别是对于小物体，因为每个 bin 代表了很大范围的可能值。

D-FINE给出的方法是：

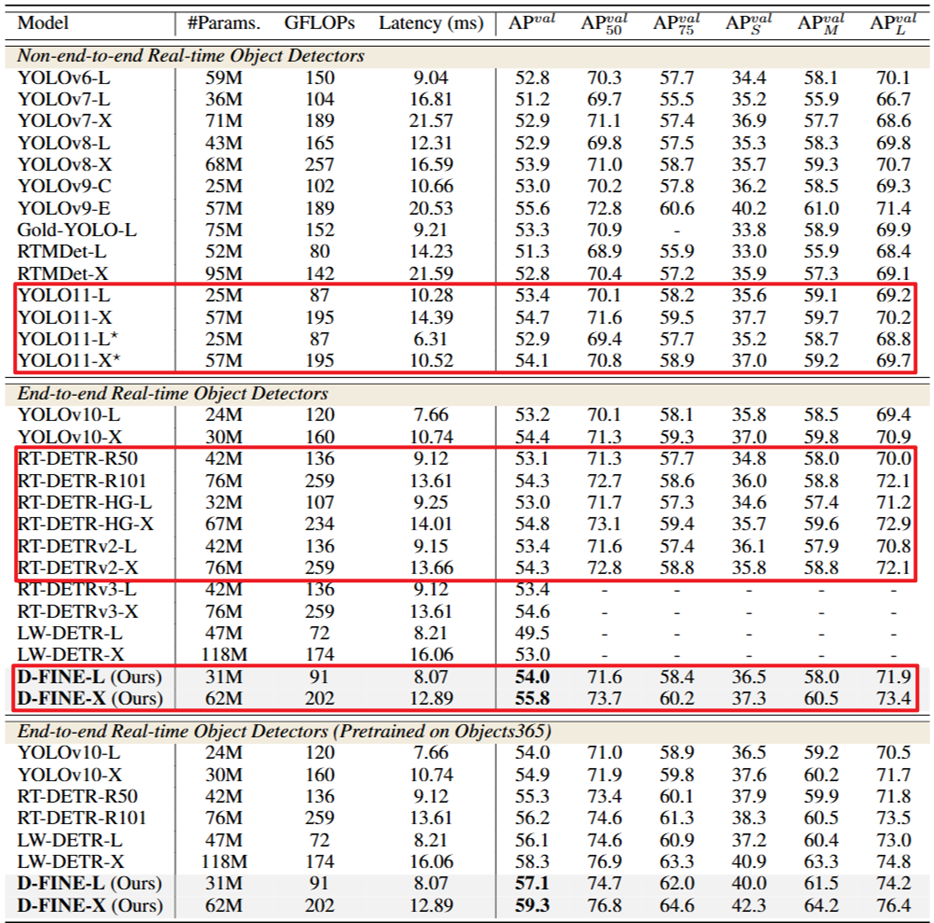
初始状态下，第一个decoder层通过传统的bounding box regression head和一个D-FINE head（两个head都是MLP，只是输出维度不同）预测初步的bounding box和初步的概率分布。每个bounding box与四个分布相关联，每个边对应一个分布。初始的bounding box作为参考框，随后的层侧重于通过以残差的方式调整分布来优化它们。然后，将细化的分布用于调整相应初始bounding box的四个边，从而在每次迭代中逐步提高其准确性。

初步的bbox的形式为$b_0 = \{x, y, W, H\}$，然后将 $b_0$ 转换为中心坐标 $c_0 = \{x, y\}$ 和边缘距离 $d_0 = \{t, b, l, r\}$，它们表示从中心到顶部、底部、左侧和右侧边缘的距离。

第 $l$ 层，refined edge distances $d_l = \{t_l, b_l, l_l, r_l\}$ 的计算公式如下： $d_l = d_0 + \{H, H, W, W \} \cdot \sum_{n=0}^{N} W(n) P_{r_l}(n), l \in \{1, 2, ..., L\},$

• 其中 $P_{r_l}(n) = \{P_{r_l}^t(n), P_{r_l}^b(n), P_{r_l}^l(n), P_{r_l}^r (n)\}$ 表示四个独立的分布，每个边缘对应一个分布。每个分布预测相应边缘的候选偏移值的可能性。这些候选值由 weighting function $W(n)$ 确定，其中 $n$ 索引 $N$ 个 discrete bins，每个 bin 对应于一个 potential edge offset。
• 分布的加权和产生 edge offsets。这些 edge offsets 然后按初始 bounding box 的高度 $H$ 和宽度 $W$ 缩放，确保调整与 box size 成比例。

概率分布 $P_r^l(n)$ 的更新通过以下公式进行：

$$P_r^l(n) = Softmax(\text{logits}^l(n)) = \text{Softmax}(\Delta \text{logits}^l(n) + \text{logits}^{l-1}(n)) \quad(3)$$

其中，$\text{logits}^{l-1}(n)$ 是前一层的 logits，$\Delta \text{logits}^l(n)$ 是当前层预测的残差 logits。

为了方便精确和灵活的调整，权重函数 $W(n)$ 定义如下： $W (n) = \begin{cases} 2 \cdot W (1) = -2a & n = 0 \\ c - c \cdot \frac{a}{c + 1} \cdot \frac{N - 2n}{N - 2} & 1 \leq n < \frac{N}{2} \\ -c + c \cdot \frac{a}{c + 1} \cdot \frac{-N + 2n}{N - 2} & \frac{N}{2} \leq n \leq N - 1 \\ 2 \cdot W (N - 1) = 2a & n = N, \end{cases}$

其中，$a$ 和 $c$ 是控制函数上界和曲率的超参数。如图2所示，$W(n)$ 的形状确保了当边界框预测接近准确时，$W(n)$ 中的小曲率允许更精细的调整。相反，如果边界框预测远非准确，则边缘附近较大的曲率和 $W(n)$ 边界处的急剧变化确保了进行大幅校正的足够灵活性。

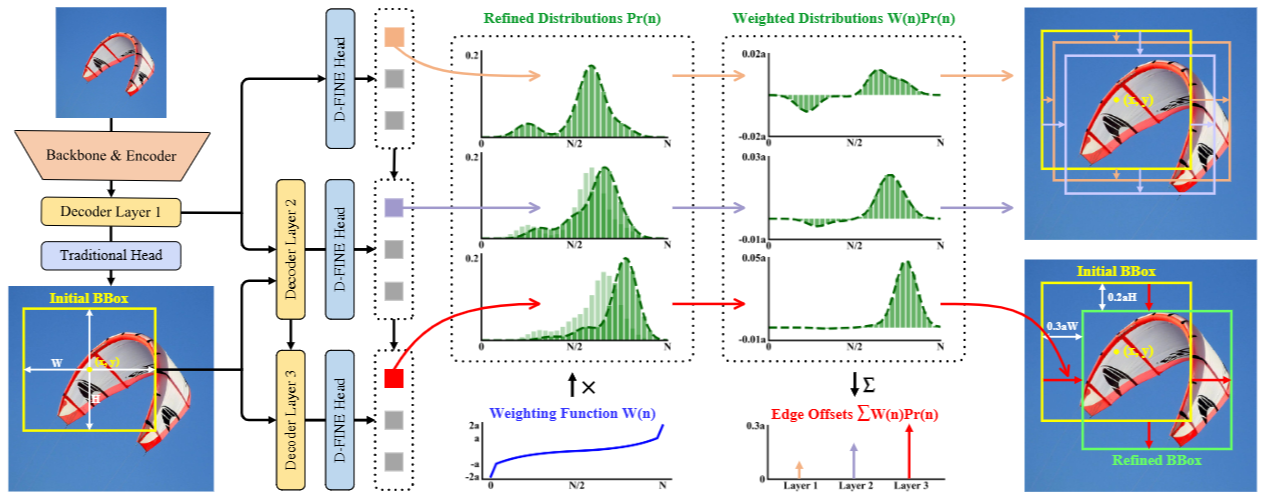
Fine-Grained Localization (FGL) Loss，这是一种新的损失函数，旨在提高 D-FINE 模型中概率分布预测的准确性，并使其与真实值对齐。

$$L_{FGL} = \sum_{l=1}^{L} \sum_{k=1}^{K} IoU_k \cdot \bigg( \omega_{\leftarrow} \cdot CE(P_r^l(n)_k, n_{\leftarrow}) + \omega_{\rightarrow} \cdot CE(P_r^l(n)_k, n_{\rightarrow}) \bigg)$$

公式 (5) 详细解释如下：

$L_{FGL}$: Fine-Grained Localization Loss，即细粒度定位损失，是该公式要定义的损失函数。

$\sum_{l=1}^{L}$: 对所有解码器层（Decoder Layers）进行求和，$L$ 表示解码器层的总数。这意味着 FGL 损失是在所有解码器层上计算的。

$\sum_{k=1}^{K}$: 对每层中的所有预测（predictions）进行求和，$K$ 表示预测的总数。这意味着对每个预测都计算损失。

$IoU_k$: 第 $k$ 个预测的 Intersection over Union (IoU)。IoU 用于衡量预测边界框与真实边界框之间的重叠程度。通过引入 IoU，可以使损失函数更加关注那些定位更准确的预测，提高整体的检测性能。

$\omega_{\leftarrow}$: 权重，用于加权左侧 bin 的交叉熵损失。 $CE(P_r^l(n)_k, n_{\leftarrow})$: 交叉熵损失（Cross-Entropy Loss），用于衡量预测的概率分布 $P_r^l(n)_k$ 与左侧 bin $n_{\leftarrow}$ 之间的差异。

$\omega_{\rightarrow}$: 权重，用于加权右侧 bin 的交叉熵损失。 $CE(P_r^l(n)_k, n_{\rightarrow})$: 交叉熵损失，用于衡量预测的概率分布 $P_r^l(n)_k$ 与右侧 bin $n_{\rightarrow}$ 之间的差异。

$P_r^l(n)_k$: 第 $l$ 层第 $k$ 个预测的概率分布。

$n_{\leftarrow}, n_{\rightarrow}$: 相邻于 $\phi$ 的两个 bin 的索引，分别代表左侧和右侧的 bin。

$\phi$: 相对偏移量，计算公式为 $\phi = \frac{d_{GT} - d_0}{\{H, H, W, W\}}$。其中，$d_{GT}$ 是 ground truth 边缘距离，$d_0$ 是初始预测的边缘距离，$H$ 和 $W$ 分别是 bounding box 的高度和宽度。相对偏移量用于将预测的偏移量归一化到 bounding box 的尺寸，使其具有相对性。 $\omega_{\leftarrow} = \frac{|\phi - W(n_{\rightarrow})|}{|W(n_{\leftarrow}) - W(n_{\rightarrow})|}$ $\omega_{\rightarrow} = \frac{|\phi - W(n_{\leftarrow})|}{|W(n_{\leftarrow}) - W(n_{\rightarrow})|}$ 这两个公式用于计算权重 $\omega_{\leftarrow}$ 和 $\omega_{\rightarrow}$，它们基于相对偏移量 $\phi$ 与相邻 bin 的加权值之间的距离。$W(n_{\leftarrow})$ 和 $W(n_{\rightarrow})$ 分别是左侧和右侧 bin 的加权函数值。这些权重用于在计算损失时，对 $\phi$ 附近的两个 bin 进行加权，使得损失函数能够更精确地反映预测的偏移量与真实值之间的差距。

总而言之，FGL Loss 通过结合 IoU-based weighting 和交叉熵损失，使得模型在训练过程中更加关注定位准确的预测，并能够精确地调整概率分布，从而实现更精确和可靠的边界框回归。 该损失函数的设计灵感来源于 Distribution Focal Loss (DFL) Generalized Focal Loss: learning qualified and distributed bounding boxes for dense object detection，DFL 通过学习 qualified and distributed bounding boxes 来改进物体检测的性能。D-FINE 的 FGL Loss 在此基础上进行了改进，通过细粒度的定位损失来进一步提升定位精度。

全局最优定位自蒸馏 (GO-LSD)

局部信息蒸馏(Localization Distillation, LD)是一种很有前途的方法，它表明迁移定位知识对于检测任务更有效(Zheng et al., 2022)。它建立在GFocal的基础上，通过从教师模型中提取有价值的定位知识来增强学生模型，而不是简单地模仿分类 logits 或特征图。尽管该方法具有优势，但它仍然依赖于基于anchor的架构，并且会产生额外的训练成本。

全局最优定位自蒸馏（GO-LSD）利用最后一层经过提炼的分布预测，将定位知识提炼到较浅的层中，如图3所示。这个过程首先对每一层的预测应用 Hungarian Matching (Carion et al., 2020)，从而识别模型每个阶段的局部边界框匹配。为了执行全局优化，GO-LSD 将所有层的匹配索引聚合到一个统一的并集中。这个并集结合了跨层最准确的候选预测，确保它们都能从蒸馏过程中受益。除了优化全局匹配之外，GO-LSD 还在训练期间优化未匹配的预测，以提高整体稳定性，从而提高整体性能。尽管定位是通过这个并集进行优化的，但分类任务仍然遵循一对一的匹配原则，确保没有冗余框。

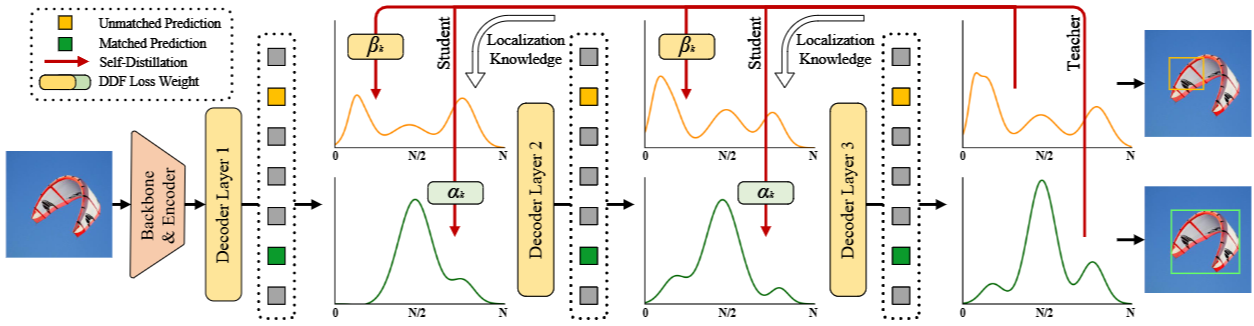
引入了解耦蒸馏焦点 (DDF) 损失，它应用解耦的加权策略，以确保为具有高 IoU 但低置信度的预测赋予适当的权重。DDF 损失还根据匹配和未匹配预测的数量对其进行加权，从而平衡它们的总体贡献和个体损失。这种方法可以实现更稳定和有效的蒸馏。解耦蒸馏焦点损失 $L_{DDF}$ 的公式如下：

$$L_{DDF} = \frac{T}{2L-1} \sum_{l=1}^{L-1} \left( \sum_{k=1}^{K_m} \alpha_k \cdot KL(P_r^{(l)(n)_k}, P_r^{(L)(n)_k}) + \sum_{k=1}^{K_u} \beta_k \cdot KL(P_r^{(l)(n)_k}, P_r^{(L)(n)_k}) \right)$$

info

$L_{DDF}$: 解耦蒸馏Focal Loss。 $T$: 温度系数，用于平滑 logits。 $L$: 总层数。 $l$: 当前层索引。 $K_m$: 匹配的预测框数量。 $K_u$: 未匹配的预测框数量。 $\alpha_k$: 第k个匹配预测的权重，计算公式为 $\alpha_k = IoU_k \cdot \frac{\sqrt{K_m}}{\sqrt{K_m} + \sqrt{K_u}}$。 $\beta_k$: 第k个未匹配预测的权重，计算公式为 $\beta_k = Conf_k \cdot \frac{\sqrt{K_u}}{\sqrt{K_m} + \sqrt{K_u}}$。 $KL(\cdot, \cdot)$: Kullback-Leibler 散度，用于衡量两个概率分布之间的差异。 $P_r^l(n)_k$: 第 $l$ 层第 $k$ 个预测的概率分布。 $P_r^L(n)_k$: 最终层（第 $L$ 层）第 $k$ 个预测的概率分布，被视为“soft label”

实验结果